2011年数学高考总复习：集合

北京四中网校独家提供

知识网络

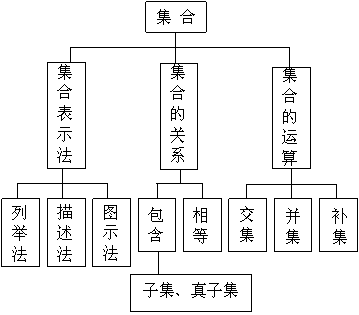
目标认知

考试大纲要求：

1. 了解集合的含义、元素与集合的“属于”关系； 能用自然语言、图形语言、集合语言（列举法或描

述法）描述不同的具体问题.

2. 理解集合之间包含与相等的含义，能识别给定集合的子集；在具体情境中，了解全集与空集的含义.

3. 理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集；理解在给定集合中一个子集

的补集的含义，会求给定子集的补集；能使用韦恩图（Venn）表达集合的关系及运算.

高考考点分析：

集合是高中数学的重要基础知识，它贯穿于整个中学数学教学之中，并且作为一种数学语言和工具在其他数学问题中有广泛的应用，在高考中，它也是年年必考的内容之一，集合问题一般有两种类型，一是涉及集合本身的问题；二是以集合为载体，综合其他数学知识构成的综合题。

1．对于集合概念的认识与理解，重点是对集合的识别与表达.

2．对集合知识的综合应用，重点考查准确使用数学语言的能力以及运用数形结合思想解决问题的能力.

重点：

对集合的识别与表达，集合的运算.

难点：

以集合为载体，综合其他数学知识的应用.

知识要点梳理

知识点一：集合的含义与表示：

1、集合的含义

一般地，我们把研究对象统称为元素，把一些元素组成的总体叫做集合(简称为集)．集合中的元素具有确定性、互异性和无序性三个特征．

确定性—— 对于任何一个对象，都能确定它是不是某一给定集合的元素。如果a是集合A的元素，就说

a属于集合A，记作a∈A；如果a不是集合A的元素，就说a不属于集合A，记作。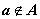

互异性—— 一个给定集合中所含的任何两个元素都是不同的对象，即在一个集合中，元素没有重复现

象。

无序性—— 在同一集合中，不考虑元素之间的顺序。

2、一些常用集合的记法：

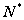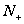自然数集记为N；正整数集记为或；整数集记为Z；有理数集记为Q；实数集记作R；复数集记作C；不含任何元素的集合叫做空集，记作。

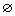3、常用的集合表示法

常用的集合表示法有：列举法、描述法、Venn图．

列举法：把集合中的元素一一列举出来，写在大括号内表示集合的方法。

描述法：把集合中元素的公共属性描述出来，写在大括号内表示集合的方法，其具体形式如下：{元素

的一般形式|元素所具有的公共属性}

Venn图：用平面上封闭曲线的内部代表集合。

知识点二：集合与集合的关系

1. 子集：

如果集合A中任何一个元素都是集合B中的元素，则称集合A为集合B的子集，记作：．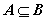

2. 相等：

若AB且B A，则集合A与集合B的元素是一样的，则称集合A与集合B相等，记作A=B．

3. 真子集：

如果集合A B ，但存在元素x∈B，且x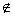A，则称集合A为集合B的真子集，记作：A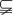B．

4. 空集：

空集是任何集合A的子集，即 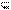A； 空集是任何非空集合B的真子集，即 B。

5. 任何集合是它本身的子集：

对于任一集合A，有A A．

6. 集合的传递性：

对于集合A，B，C，如果A B，且B C，则A C．

7. 含n个元素的集合的子集个数

含n个元素的集合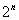有个子集，有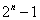个真子集，有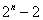个非空真子集．(同学们可结合组合的有关知识予以证明)．

知识点三：集合的运算

1. 交集：

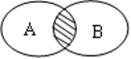
对于两个给定的集合A、B，由属于A且属于B的所有元素组成的集合，叫做A与B的交集，记作A∩B.即A∩B={x|x∈A且x∈B}。

Venn图表示：（阴影部分代表集合A与集合B的交集）；

性质：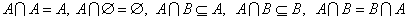

2. 并集：

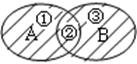
对于两个给定的集合A、B，由属于A或属于B的所有元素组成的集合，叫做A与B的并集，记作A∪B.即：A∪B={x|x∈A或x∈B}；

Venn图表示：（阴影部分表示A与B的并集）

性质：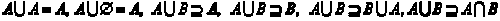

注意：并集中的元素可分为三类：

第一类是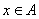但；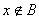

第二类是；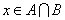

第三类是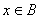但.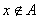

3. 全集与补集

全集：在研究集合与集合之间的关系时，如果一个集合含有我们所研究问题中涉及的所有元素，那么这个集合就称为全集，通常用U来表示.

补集：对于一个集合A，由全集U中所有属于U但不属于A的元素组成的集合称为集合A相对于全集U的补集，记作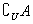. 即：.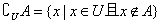

Venn图表示：（阴影部分表示A在I中的补集 ）

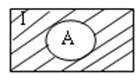
性质：，.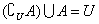

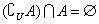注意：

（1）全集是相对所研究问题而言的一个相对概念，因研究问题不同全集也不同.例如在研究数集时，

常把实数集R看作全集；在平面几何中，整个平面可以看作全集.

（2）如下图所示韦恩图中，